Excel SOLVER Add in with Examples

Excel SOLVER Add in with Examples

Managers of companies want to find the optimum solutions to practical problems. They want to find certain values for a cell that optimize particular objective. To provide hands on solutions to this kind of optimization problems, Microsoft has introduced Excel Solver Add in, which helps to find optimal value for a formula subject to constraints, or limits on the values of other formula cells on a worksheet.

In this section:

---

1. What is Excel Solver?
2. How to install SOLVER Add in?
3. Solving Optimization Problems without Constraints.
4. Solving Optimization Problems with Constraints.
5. Solving Budgeting Problems with Constraints.
6. Practical Exercise.

---

---

1. What is Excel SOLVER?

To perform what-if analysis Excel has introduced an add-in, which is called SOLVER. Solver is used to find optimal (maximum or minimum) value for a formula in one cell, the objective cell, subject to constraints, or limits, on the values of other formula cells on a worksheet. Solver works with a group of cells, called decision variables or simply variable cells that are used in computing the formulas in the objective and constraint cells. Solver adjusts the values in the decision variable cells to satisfy the limits on constraint cells and produce the result users want for the objective cell.

2. How to Install SOLVER?

Your first job is to check whether you already have the SOLVE installed in your Excel. To do so, you need to follow the steps below:
Step 1: Click on Data Tab

Step 2: Took at the top-right corner and check whether you can see the Solver (as shown in the above image)

After checking the status of the SOLVER, if you do not see it on the top-right corner, you are required to install the add-in. To install, you need to follow the steps below:

Step 1: Click on File Tab–Then click on Option. Now, you can see the Excel Options dialogue box.

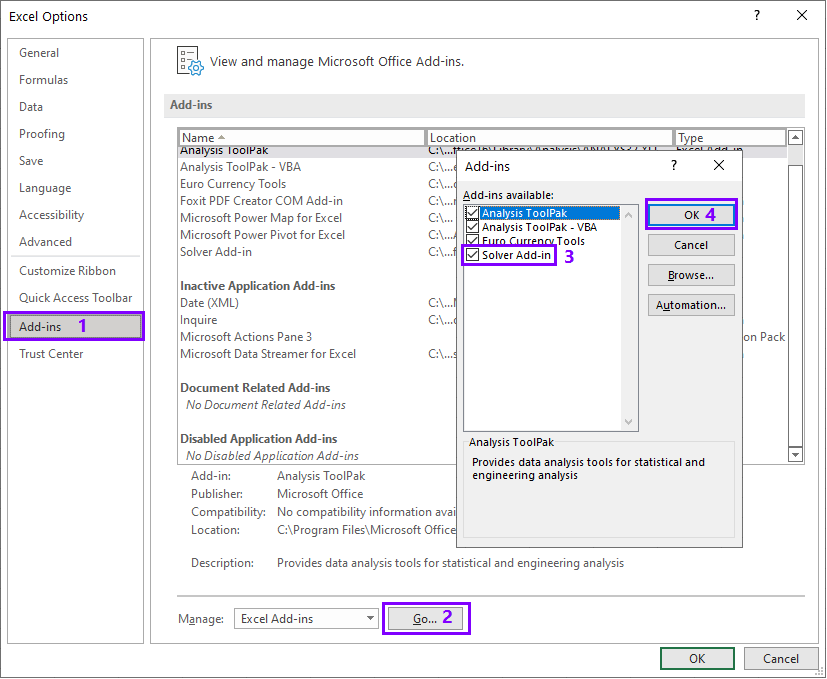
On the dialogue box, (1) click on add-in –> (2) click on Go–> (3) Check Solver Add-in, and –> (4) Click OK.

3. Solving Optimization Problems without Constraints:

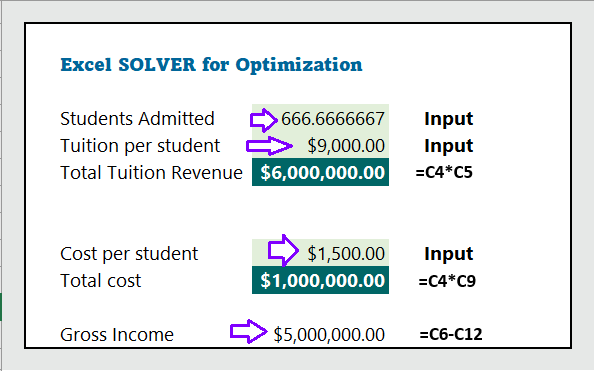
The Problem: We have the following data related to university student admission, tuition revenue, cost per student, and gross income. We want to earn total $5,000,000 gross income. What is the best solution?

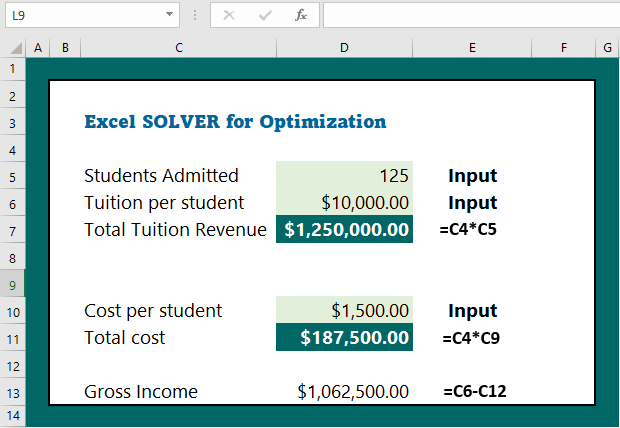
Solutions: To solve this problem, we need to follow the steps below:

Step 1: Start the SOLVER. To do so, click on Data Tab–> Click on Solver. After clicking on Solver, you will see the Solver Parameters as below.

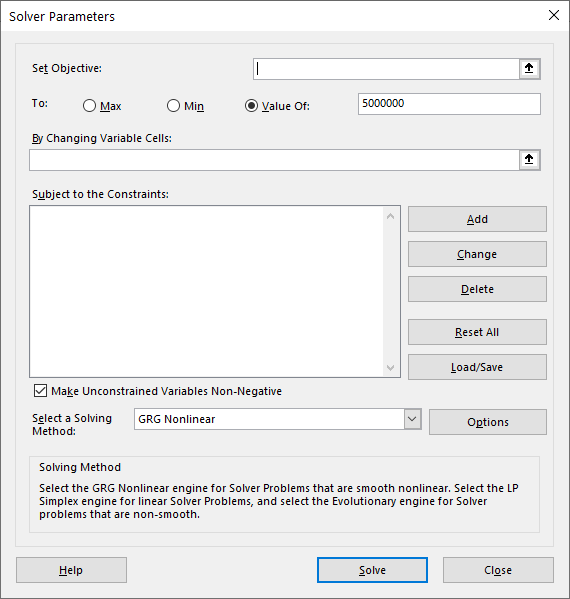
Step 2: Set the parameters:

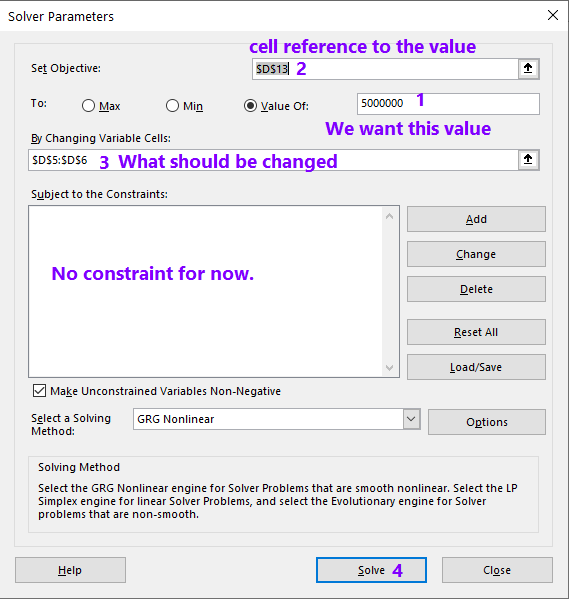
Explanation:

1. Set the value: In our example, we want to earn total gross income of $5,000,000. We checked value of and wrote the amount of $5,000,000 in the box.
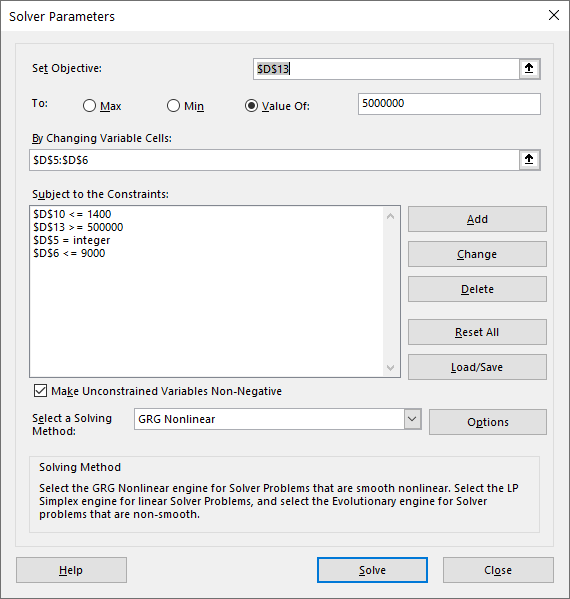
2. Set Objective: This is the cell reference of your value, which is D13. We select D13.
3. Changing Variable Cells: We want to change the number of students admitted and the tuition per student, and the cell reference is D5 and D6. We selected D5:D6.
4. Solve: Now, we click on “Solve“.

After clicking on “Solve“, the Solver Results dialogue box will be opened, and you have two options:

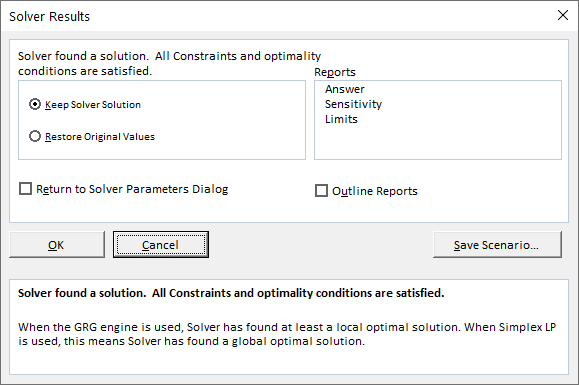
1. OK: If you like the solutions, you should click on “OK“, OR
2. If you want to change something, you can click on “Cancel“.

In our example, for now, we like the solution, and we click OK. The results are presented below:

Findings from the solutions:

1. Students Admitted: The SOLVER suggests that we need to admit 587.76 students. The problem in the number is that number of students CANNOT be fraction. We need an integer.
2. Tuition per student: Solver’s suggestion is to increase the tuition fee to $10,006.81. However, the potential problem in this solution is that we may need to decrease tuition fee if we want to admit more students.

4. Optimization Problems with Constraints:

Let’s continue with our problem. Suppose, we want to include three constrains, namely:

1. Number of students cannot be fraction–it should be an integer.
2. Tuition fee should be less than $9,000.
3. Cost per student should not be more than $1,450.

Solution:

The steps 1 and 2 are same as they are in problem 1 solved above. We need to add constraint in the step 3. To do so, we need to click on “Add” on the right side of “Subject to the Constraints“. [See image below]

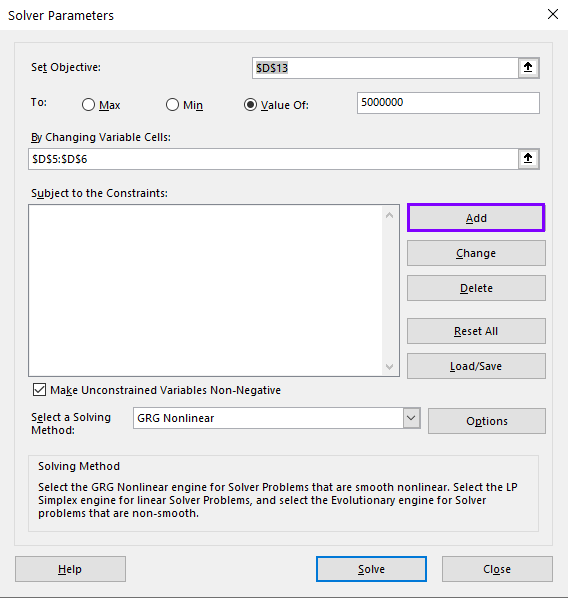
Setting the Constraints:

After clicking on “Add“, the Add Constraint dialogue box will be opened. Let’s see an example.

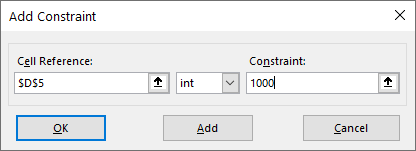
The first constraint: We want the number of students should not be a fraction. We have given:

• The reference to the student number, which is D5. We have also told solver the maximum number of students could be 1,000.
• Gross income should not be less than $5,000,000 (D13>=5,000,000)
• Tuition per student should not be less than $9,000 (D6<=9,000)
• Cost per student should not be more than $1,400 (D10<=$1,400)

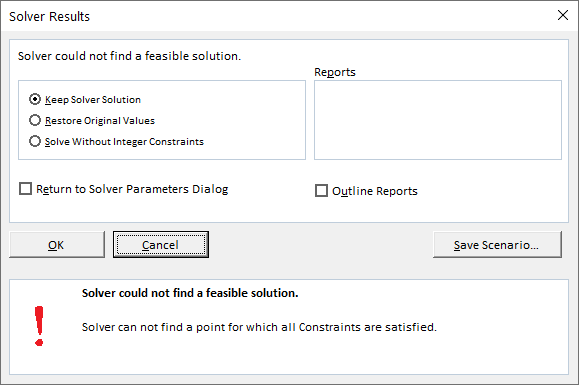
After setting the constraints, we click SOLVE, and the Solve has given the following solutions with a warning!!

What next?

We found two issues: (1) number of students is still a fraction, (2) cost per student is still $1,500. We can reset the constraints to find an optimum solution.

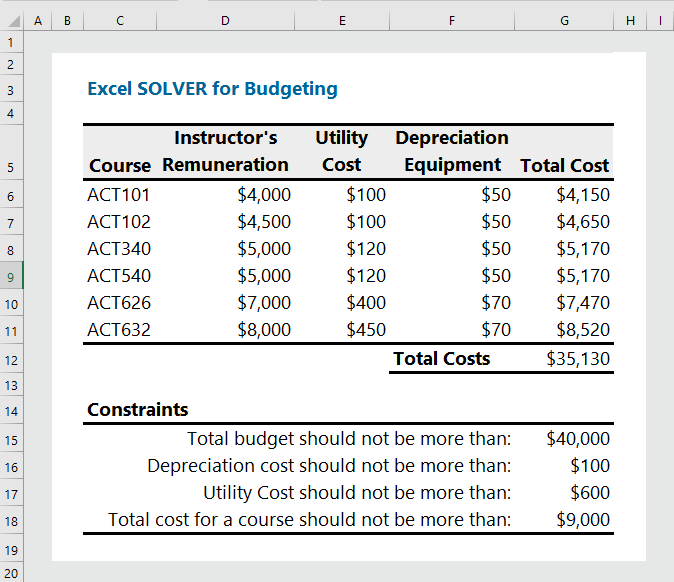
5. Solving Budgeting Problems with Constraints:

The Problem:

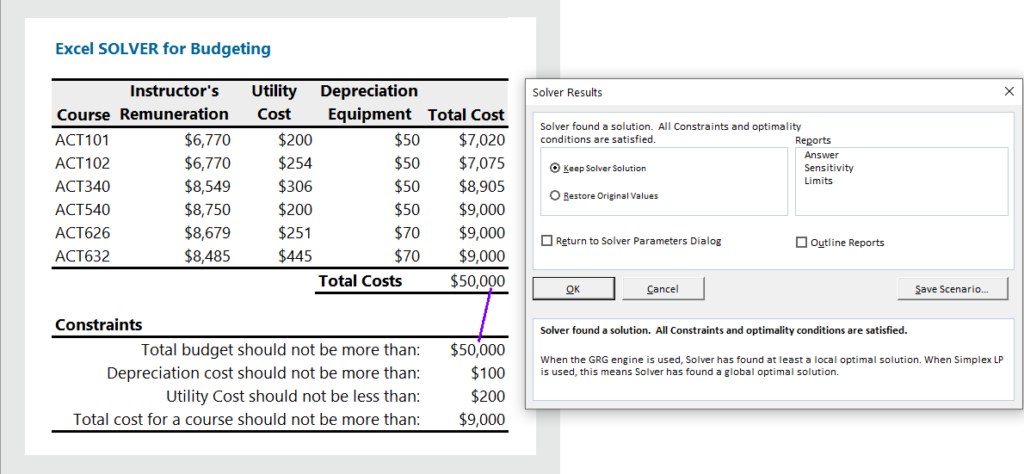
The department of Accounting at the University of Texas is planning budget for six accounting courses. The total budget for the six courses offered in Fall-2022 is $50,000. The administration wants to allocate the total budget of $50,000 to all the courses. The expected instructors’ remuneration, utility cost, depreciation of equipment, total cost per course, and potential constraints are given in the following tables.

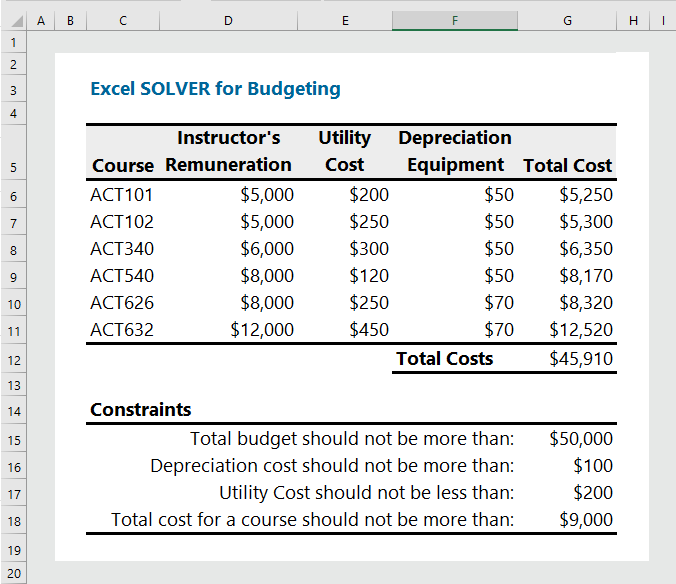
You are required to:

1. Use Excel SOLVER to allocate the total $50,000 to all the courses.
2. While solving this problem, you have to consider the following constraints:
   • Total budget should not be more than $50,000.
   • Depreciation should not be more than $100.
   • Minimum utility cost per course is $200.
   • Total cost for a course should not exceed $9,000.

Solution:

Step 1: Start the Excel Solver:

Click on Data Tab–> Then click on Solver.

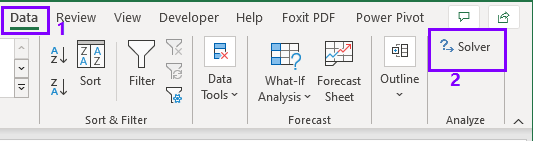
After opening the Solver Parameters dialogue box,

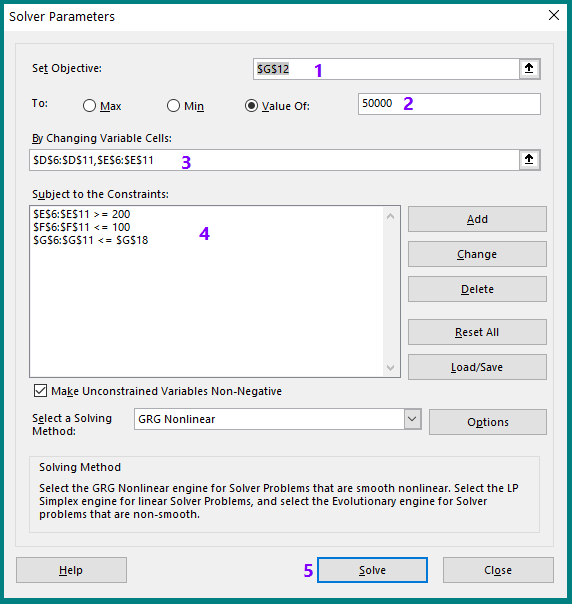
Step 2: Set Objective:

The target cell is G12, which should not exceed the value of $50,000. We therefore, select G12 (1 in image) and set the value of $50,000 (2 in image).

Step 3: Set the Changing variables:

We can change:

(I) Instructors’ remuneration in cell D6:D11 (we select D6:D11 as 3 in image below)

(II) Utility cost in cell E6:E11 ( we select E6:E11 as 3 in image below)

Step 4: Setting constraints:

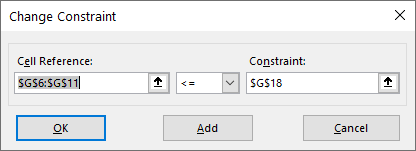
I) Depreciation should not be more than $100, indicating that F6:611<=100.

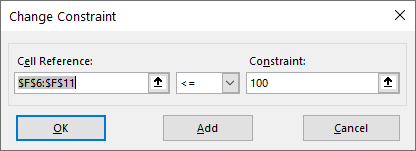
II) Utility cost should be more than $200, indicating that E6:E11>=$200.

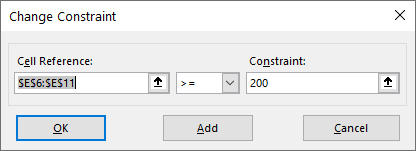
III) Total cost of a course should not be more than $9,000, indicating that G6:G11<= G18

Step 5: Click on Solve.

Then you can see the solver results dialogue box as follows:

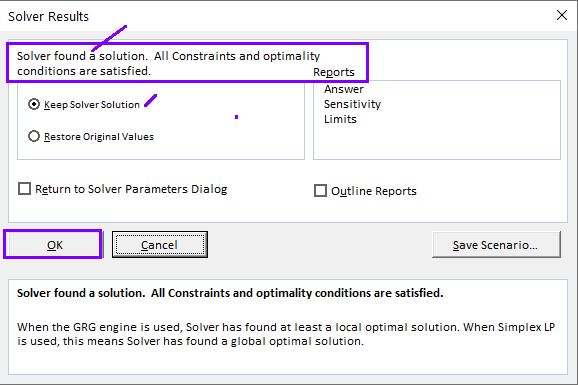
You can check whether you will go with the solutions. We can see in the following image that all constraints have been satisfied. You just click OK and keep the solver solutions.

Exercise:

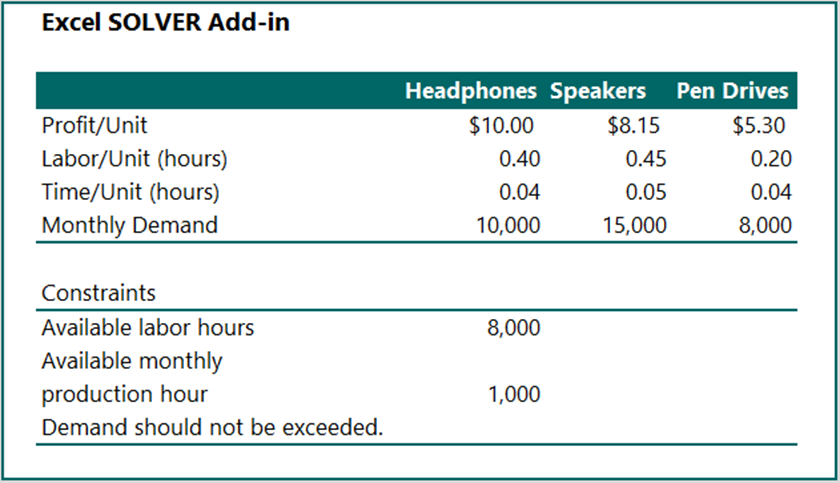
Optimal Product Mix:

Maxwell Technology produces headphones, speakers, and pen drives. Maxwell’s total monthly available hours is 8,000 whereas monthly production hour is 1,000. The profit, labor, time, and monthly demand information are given in the following table. Considering monthly demand constraints for each product, how can Robert Maxwell his profit?

You are required to:

1. Solve the profit maximization problem considering the following constraints:

Constraints
Available labor hours	8,000
Available monthly production hour	1,000
Demand should not be exceeded.

2. Before running the SOLVER, prepare a projected solutions as follows:

	Headphones	Speakers	Pen Drives			Totals
Monthly production unit	9,000	5,500	6,900			21,400
Monthly Profit	$90,000	$44,825	$36,570			$171,395
Labor hours	3,600	2,475	1,380			7,455
Production hours	315	247.5	241.5			804

More resources:

Microsoft Official Post

CONCAT Function

Arraytotext function