Correlation in Excel Graph
Correlation in Excel Graph is easy and useful. In this section, we discuss how to prepare correlation in Excel graph. Excel users use Correlation in Excel to find relation between variables. The Excel CORREL function returns the correlation coefficient of two cell ranges. To determine the relationship between two variables or properties, Excel users use CORREL function. Users can examine the relationship between temperature and the number of fans sold.
In this section:
- Syntax of Excel CORREL Function.
- What is correlation?
- Example of Positive Correlation.
- Example of Negative Correlation.
- Example of Zero Correlation.
- How to Calculate Correlation Coefficients.
1. Syntax of Excel CORREL Function:
CORREL(array1, array2)
where:
- array1: The range of first cell values, and it is a required argument.
- array2: The range of second cell values, and it is a required argument.
Notes:
- If the reference argument or array contains text, logical values, or empty cells, those values are ignored; however, cells with zero values are included.
- CORREL returns a #N/A error in case users use different number of data points for array1 and array2.
- CORREL returns #DIV0! error if either array1 or array2 is empty, or if s (the standard deviation) of their values equals zero.
- If the correlation coefficient is closer to +1 or -1, it indicates a strong positive (+1) or negative (-1) correlation between the arrays.
2. What is Correlation?
When we speak about correlation, we normally speak of tendencies. We speak on the positive and negative relationships. Think about weight and height. They are positively correlated. Greater weight is associated with greater height. In statistics, correlation refers to the relationship between two properties. In other words, correlation is how two variables move in relation to another.
Example 1: If temperature increases, the sale of air conditioners increases, indicating that they are positively related.
Example 2: If the price of a product goes up, the demand for that product goes down, indicating that price and demand are negatively related.
3. Example of Positive Correlation:
When two variables move positively, it means they are positively correlated. If one of them goes up, the other one will also go up, and vice-versa.
Example of positive correlation:
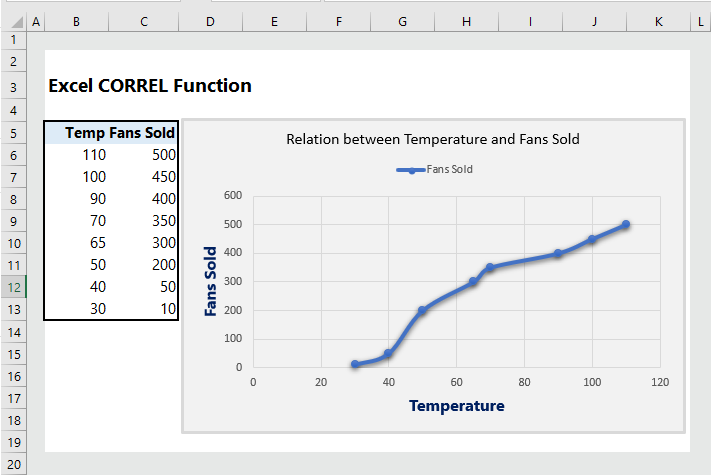
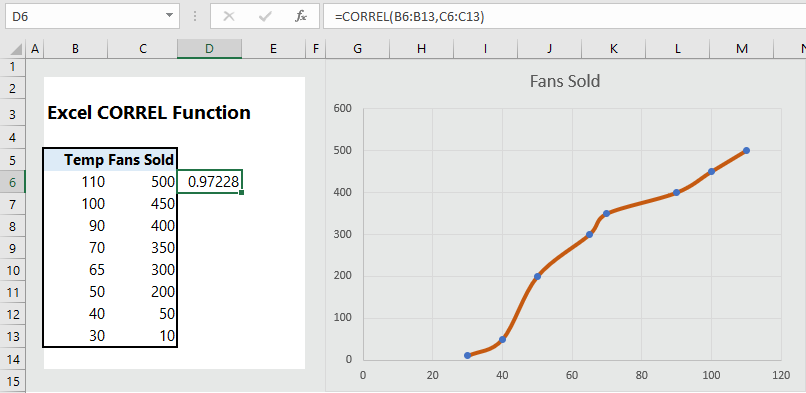
In the following table, we have the data on temperature and fans sold. The formula to calculate correlation coefficient is =CORREL(B6:B13, C6:C13), which returns the correlation coefficient of 0.972, indicating that temperature and sale of fans are positively correlated.
More examples of Positive Correlation:
- Age is positively correlated with experience.
- The shoe size is positively correlated with height of a person.
- Education level is positively correlated with income.
- Hours spend in study is positively correlated with grade points.
4. Examples of Negative Correlation:
When two variables move in the opposite direction, they are negatively correlated. If one of them moves up, the other one moves down. A perfectly negative correlation is written as -1.
Example of Negative Correlation:
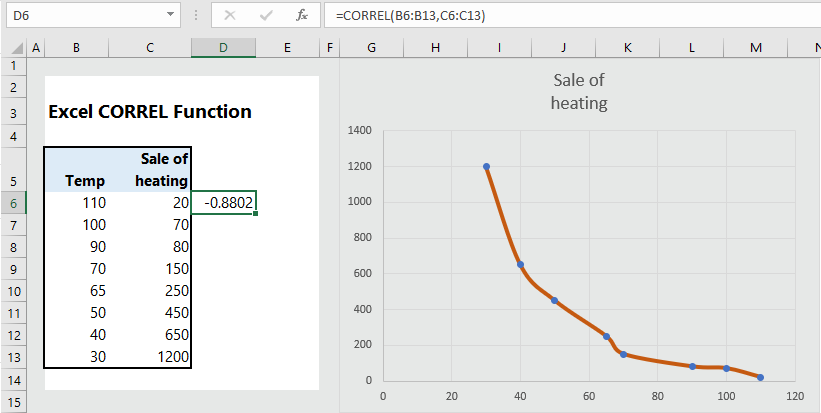
In the following table, we have the data on temperature and sale of heating machine. The formula to calculate correlation coefficient is =CORREL(B6:B13, C6:C13), which returns the correlation coefficient of -0.8802, indicating that temperature and sale of heating are negatively correlated.
More examples of negative correlation:
- Education is negatively correlated with poverty.
- Price of a product is negatively correlated with demand of that product.
- Drinking coffee is negatively correlated with tiredness.
- Sickness and health are negatively correlated.
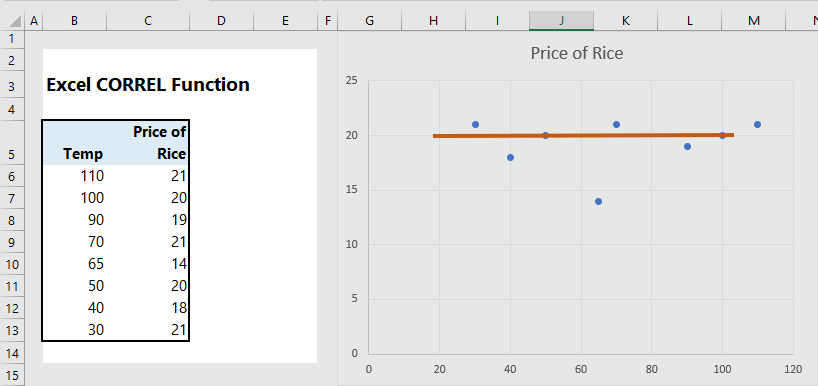
5. Example of Zero Correlation:
A zero correlation means there is no correlation between two variables. For example, if one variable moves one way, another variable moves in another way, which is unrelated.
More examples of Zero Correlation:
- One’s height and grade in exam.
- One’s height and sickness.
- Shoe size and miles driven.
- Height and income.
- Exercise and exam scores.
6. How to Calculate Correlation Coefficient:
The correlation between two variables measures the strength and direction of the linear relationship between the two variables. The correlation coefficient ranges between -1 and +1, where -1 indicates a perfect negative correlation, and +1 indicates a perfect positive correlation, and the 0 coefficient indicates no correlation. As we said, the correlation coefficient indicates the DIRECTION and the STRENGTH of the relation. Let’s take examples on how to explain the correlation coefficient.
Example 1:
In the example below, the data on temperature and sale of heating machine are given. We have calculated the correlation coefficient by using the formula =CORREL(B6:B13, C6:C13), which returns the coefficient of -0.88.
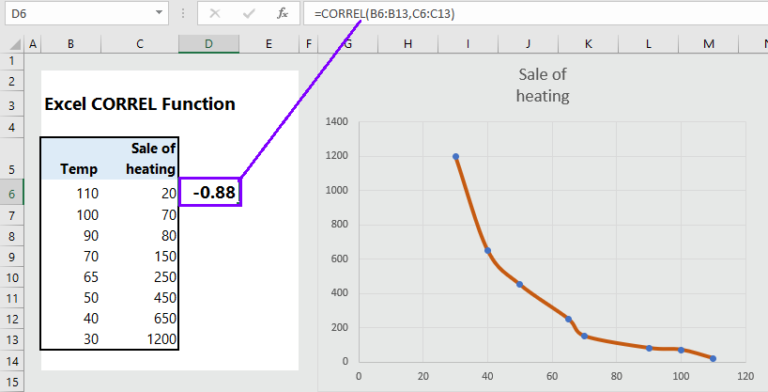
Explanation:
Direction: Temperature and Sale of heating machine are negatively associated.
Strength of relation: The relation is strong enough because the value is close to -1.
In mathematical term: For one degree increase in temperature, the sale of heating machine decrease by 0.88.
Example 2:
In the example below, the data on temperature and sale of fans are given. We have calculated the correlation coefficient by using the formula =CORREL(B6:B13, C6:C13), which returns the coefficient of 0.972.
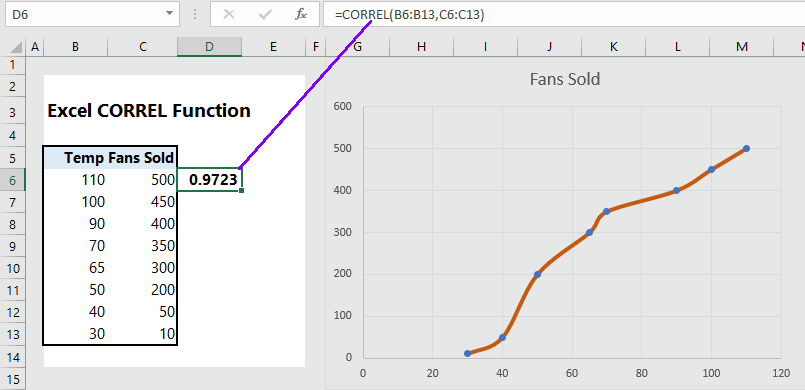
Explanation:
Direction: Temperature and Sale of fans are positively associated.
Strength of relation: The relation is strong enough because the value is close to +1.
In mathematical term: For one degrees increase of temperature, the sale of fans increase by 0.972.
More related readings:

I have been surfing online more than three hours today, yet I never found any interesting article like yours. It?s pretty worth enough for me. In my opinion, if all web owners and bloggers made good content as you did, the net will be a lot more useful than ever before.
Hey very cool blog!! Man .. Beautiful .. Amazing .. I’ll bookmark your website and take the feeds also?I am happy to find a lot of useful information here in the post, we need develop more techniques in this regard, thanks for sharing. . . . . .
Do you mind if I quote a couple of your posts as long as I provide credit and sources back to your site? My blog site is in the exact same area of interest as yours and my users would really benefit from a lot of the information you provide here. Please let me know if this okay with you. Appreciate it!